Median of Two Sorted Arrays

Posted on |

问题描述（难度困难）

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example 1:

1
2
3
4
nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Example 2:

1
2
3
4
nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

方法一：归并排序思想

归并排序在merge之后会将各个有序的子数组合并为一个数组，这里采用归并排序sort的思想，时间和空间复杂度为O(m+n)。用两个index去遍历，每次将最小的整合到一个新的list中，直到整个都遍历完成，需要注意当一个列表遍历完成之后的极端情况。整合的流程如下：

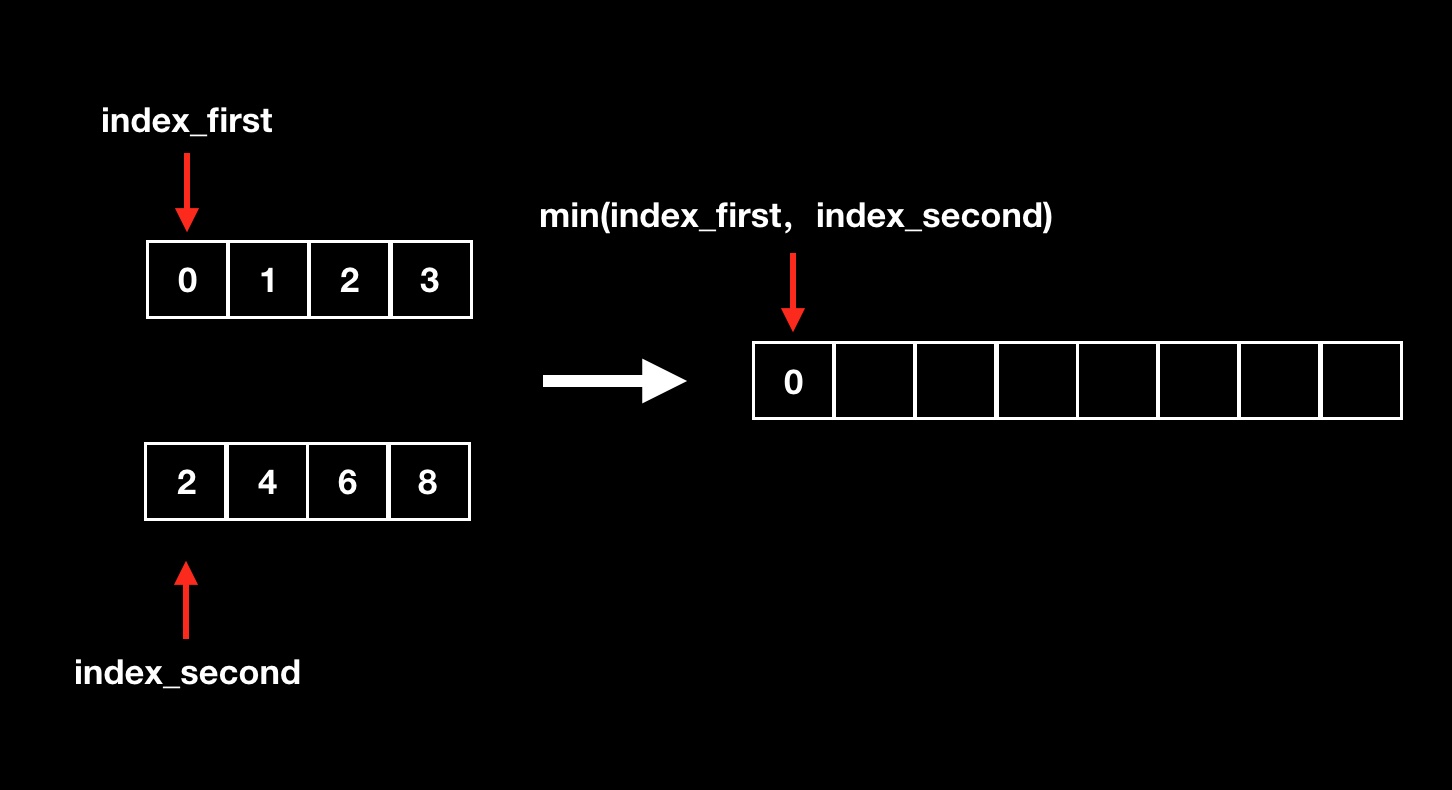
cmd-markdown-logo

方法一代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
       int length = nums1.length + nums2.length;
       ArrayList<Integer> arrayList = new ArrayList();
       int index1 = 0, index2 = 0;
       for (int i = 0; i < length; i++) {
           if (index1 > nums1.length - 1) {
               arrayList.add(nums2[index2]);
               index2++;
           } else if (index2 > nums2.length - 1) {
               arrayList.add(nums1[index1]);
               index1++;
           } else {
               if (nums1[index1] < nums2[index2]) {
                   arrayList.add(nums1[index1]);
                   index1++;
               } else {
                   arrayList.add(nums2[index2]);
                   index2++;
               }
           }
       }

       int mid = length / 2;
       if ((length & 1) == 0) {
           return (arrayList.get(mid) + arrayList.get(mid - 1)) / 2.0;
       } else {
           return arrayList.get(mid);
       }
   }

方法二：固定和双指针遍历

方法一中我们其实是把问题转换为了归并排序归并问题，但是实际上并不需要扫描全部的记录，并且也不需要存储整合之后排序的所有的结果，时间复杂度为O(min(m,n)/2，leetcode上大部分说是O(log(min(m,n)))，可能理解还不够到位，先记录下吧，空间复杂度为1。这里介绍另一种方式：

cmd-markdown-logo

大概的思路就是两个数组都维持一个索引位置，两个索引位置需要满足index_first+index_second=(length1+length2-1)/2-1，只有当first_left小于second_right并且second_left小于first_right的时候表示找到了中位数的位置，不然改变其中一个的位置。感觉这个公式还是蛮难理解的，可以理解为在两个数组之间画一条分割线，分割在中间就需要满足index=(length-1)/2。

这里还需要注意一种情况就是当index_first==-1和index_second==-1时first_left和second_left用Integer.MIN_VALUE代替，index_first == length1-1和index_second=length2-1时first_right和second_right用Integer.MAX_VALUE代替。

方法二代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
//1.记录当前划分位置的前后节点
    private ArrayList<Integer> tempArray=new ArrayList<>();

    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length;
        int length2 = nums2.length;
        int length = length1 + length2;
        if (length1 == 0 && length2 > 0) {
            return (nums2[length2 / 2] + nums2[(length2 - 1) / 2]) / 2.0;
        } else if (length2 == 0 && length1 > 0) {
            return (nums1[length1 / 2] + nums1[(length1 - 1) / 2]) / 2.0;
        } else {
            //2.若数组的长度为length1，那么分割数组的index位置为(length-1)/2,那么这里整个数组的分割位置为(length-1)/2,减去numsIndex1，但是因为数组是分成了两个，这里需要额外减去1
            int numIndex1 = (length1 - 1) / 2;
            int numIndex2 = (length - 1) / 2 - numIndex1 - 1;

            while (true) {
                //3.边界值，最左边==-1的边界值left设置为Integer.MIN_VALUE，最右边的边界值right==length-1设置为Integer.MAX_VALUE
                setLeftAndRight(numIndex1,nums1);
                setLeftAndRight(numIndex2,nums2);
                //4.比较更加直观
                Integer nums1Left=tempArray.get(0),nums1Right=tempArray.get(1),nums2Left=tempArray.get(2),nums2Right=tempArray.get(3);
                //5.满足截取的位置条件，数组一分割位置左边的元素小于数组二分割位置右边的元素，数组二分割位置左边的元素小于数组一分割位置右边的元素。
                if (nums1Left <= nums2Right && nums2Left <= nums1Right) {
                    //6.判断整个length的长度是否为偶数
                    int temp = length & 1;
                    if (temp == 1) {
                        return findMax(nums1Left, nums2Left) / 1.0;
                    } else {
                        return (findMax(nums1Left, nums2Left) + findMin(nums1Right, nums2Right)) / 2.0;
                    }
                } else if (nums1Left > nums2Right) {
                    numIndex1--;
                    numIndex2++;
                } else {
                    numIndex1++;
                    numIndex2--;
                }
                tempArray.clear();
            }
        }
    }
    private void setLeftAndRight(int index, int[] nums){
        int left,right;
        if (index == -1) {
            left = Integer.MIN_VALUE;
            right = nums[index + 1];
        } else if (index == nums.length- 1) {
            left = nums[index];
            right = Integer.MAX_VALUE;
        } else {
            left = nums[index];
            right = nums[index + 1];
        }
        tempArray.add(left);
        tempArray.add(right);
    }
    private int findMax(int a, int b) {
        return a > b ? a : b;
    }

    private int findMin(int a, int b) {
        return a > b ? b : a;
    }

总结

两种方式感觉还是第一种理解和书写上更加简单明了，第二种方式在理解和书写上相对困难，而且实际表现出的性能优化也没有特别夸张，可能在非常大的数据量上会表现更加好。